Before reading this tutorial, you should already be familiar with the concepts of an arithmetic mean, a z-score, sampling distributions, and null hypothesis significance testing. If you are unfamiliar with arithmetic means, see the tutorial on Mean, Median, and Mode. If you are unfamiliar with z-scores, see the tutorial on Dispersion. If you are unfamiliar with sampling distributions, see the tutorial on Sampling. If you are unfamiliar with null hypothesis significance testing, see the tutorial on Hypothesis Testing.
As you might have guessed on the basis of the title of this tutorial, the concept of t-distributions is used quite frequently in hypothesis testing. Specifically, the t-distribution is often referred to when comparing the means of two groups of individuals, or when comparing the mean of one group of individuals to some predetermined standard.
In this tutorial you will examine the following concepts:
Suppose a researcher at State University wants to know how satisfied students are with dormitory living. The researcher administers a survey where students answer questions on a scale of 1 to 7 with 1 representing very unsatisfied with dormitory living and 7 representing very satisfied with dormitory living. The researcher wants to know if students at State University have feelings about dormitory living that are not neutral.
How can the researcher tell whether the State University students demonstrate an attitude that is not neutral? To answer this question, the researcher will collect a sample of students who live in dormitories and ask them how satisfied they are with dorm life. The researcher collects a sample because it is typically not economically feasible to survey all members of a population. Having collected the sample, the researcher will then compute the mean level of satisfaction in the sample. Chances are that the sample mean will not be exactly 4 (i.e., neutral). Therefore, the researcher has to determine if the sample mean deviates from 4 due to sampling error, or if the sample mean deviates from 4 because the population of dormitory students are not neutral about dorm life. Let's assume that the researcher samples 15 students, that the sample mean is 5.0, and that the sample standard deviation is 1.936.
The question the researcher must answer is whether, given sampling error, 5.0 is far enough away from 4 to conclude that college students at State University are not neutral about dorm living. To make this decision, the researcher must rely on the concept of the sampling distribution of the mean for the population. For this particular problem, the researcher needs to estimate the sampling distribution and the associated standard error (i.e., the standard deviation of the sampling distribution) when the sample size is 15 students.
One way to estimate the sampling distribution directly is to survey all dormitory students at the university (i.e., sample the entire population) and create the actual sampling distribution from all possible random samples of 15 students. However, if the researcher samples the entire population, then there is no need to create the sampling distribution for N = 15. That's because the mean satisfaction rating from all the dormitory students would be the population mean and would inform the researcher exactly where the average attitude about dormitory living fell.
Remember that cost and other technical problems typically preclude
a researcher from sampling an entire population.
Therefore, the researcher must somehow estimate the sampling
distribution and standard error without surveying all members of the
population.
Fortunately, statistical research shows that when certain assumptions
are met, the sampling distribution can be estimated.
The shape of the sampling distribution for this type of problem is
different from the normal distribution, especially when sample size is
less than 30 subjects.
This sampling distribution is given the special label of the
"t-distribution".
For practical purposes, the shape of the t-distribution is identical
to the normal distribution when sample size is large.
However, when sample sizes are small (below 30 subjects),
the shape of the t-distribution is flatter than that of the normal
distribution, and the t-distribution has greater area under the tails.
The reason that the distribution is not normal is because the standard
error is estimated using the sample standard deviation instead of the
population standard deviation (because the population standard
deviation is not known).
This creates some uncertainty that is reflected in the t-distribution
having greater area under the tails than the normal distribution,
especially when the sample size is below 30 subjects.

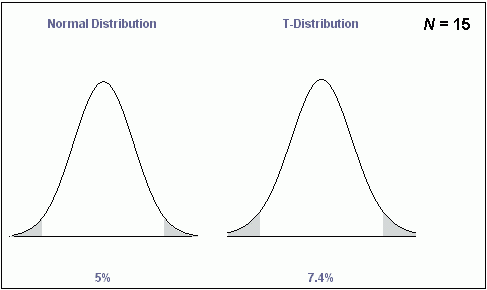
As you can see, even when the sample size is 15 subjects, it is hard to tell the two distributions apart with the naked eye. Nonetheless, the differences may be important when comparing the area under each curve at a same standard score away from the mean. Recall that it is common practice to consider a result as statistically significant only if the probability of its occuring by chance is less than 5%. The gray areas under the curves and the percentages below the pictures represent the total area of the sampling distribution above a z-score of +1.96 and below a z-score of -1.96. The z-score values of +1.96 are the critical values for a two tailed hypothesis test when using the normal distribution to represent the sample distribution. That is, if the sampling distribution were shaped as a normal distribution, 2.5% of the scores are above +1.96 and 2.5% of the scores are below -1.96 (for a total area of 5% outside of these ranges).
In contrast, for the t-distribution at sample size of 15, 3.7% of the scores are above +1.96 and 3.7% of the scores are below -1.96 (for a total area of 7.4% outside of these ranges). Therefore, when using the t-distribution, the critical values of the .05 two-tailed test must be set higher, at +2.15. This shows you that the main practical implication when using the t-distribution with sample sizes below 30 is that the critical value (i.e. the cut-off value used to decide statistical significance) is higher when using the t-distribution than when using a sampling distribution found to be shaped like a normal distribution. This is another way of saying that small sample sizes yield less certain results, and so a stronger test is imposed before claiming that a result is significant.
It is usually the case that researchers do not know the population standard deviation for the variables they are studying. Therefore, researchers are more likely to use the t-distribution than a normal distribution when testing hypotheses. Thus, the critical value used by the researcher must be related to the sample size. However, when sample sizes are greater than 30, the differences in critical values between the t-distribution and the normal-shaped sampling distribution are negligible.
Besides knowing the shape of the t-distribution, the researcher also
needs to estimate the standard error.
The standard error is the standard deviation of the sample mean.
It is important to understand that standard error is not the
standard deviation for the values of the population, nor is it the
standard deviation for the values of the sample.
Rather, standard error is a measure of the error that we expect to
find in the value obtained for the sample mean.
For a given size N, there are many different samples of that
size that can be drawn from the population.
Each such sample of size N has a mean.
It is the distribution of these sample means, and thus a measure of
the error for any one of those means, that is being described by
the term "standard error."
Of course, we only have one sample, and so one sample mean.
The standard error for this mean can be estimated using the standard
deviation for the values of the sample.
Recall that we assumed that our survey yielded a sample mean of 5.0 with a
sample standard deviation of 1.936.
To answer our dormitory question, we estimate the standard error of
the sample mean using the following formula.
|
|
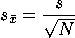 |
For our dormitory example, the standard error of the mean is .50, which is the value you get when dividing 1.936 (s, or the sample standard deviation) by the square root of 15 (i.e. the square root of N which represents the number of subjects). Again, this standard error of the sample mean is interpreted as the standard deviation of the t-distribution when the sample size is 15.
Once we recognize the shape of the t-distribution and we know the value of the standard error it is a simple matter to make a statistical decision about our survey result. The null hypothesis for this study is that students have neutral feeling about dorm life at State University. The nondirectional alternative hypothesis is that students at State university are not neutral. Recall that scientists traditionally use a 5% probability of a Type I error - that is, they want to make sure that the probability of incorrectly rejecting the null hypothesis is less than 5%. Using this 5% standard, all that is necessary is to calculate how many standard errors the sample mean is from the hypothetical population mean of 4.
The two-tailed, .05 critical t-values are +2.15 when the sample size is 15. So, the null hypothesis will be rejected in favor of the hypothesis that students are not neutral about dorm life if the observed sample mean is greater or less than 2.15 standard errors of the mean away from the hypothetical population mean of 4. Since the observed sample mean for our example is 5.0, and .50 is the standard error of the mean, then we see that the sample mean is 2.0 standard errors of the mean away from 4. It is 2.0 standard errors away because 5.0 (the sample mean) minus 4 (the population mean) equals 1.0, and 1.0 divided by .50 (the standard error of the mean) equals 2.0. Given that 2.0 is less than the critical value value of 2.15, the researcher fails to reject the null hypothesis. Based on the evidence from the sample of 15 subjects, the researcher cannot conclude that students are satisfied with dorm living. Remember that failing to reject the null hypothesis does not necessarily mean the null hypothesis is true, since the standard for rejecting the null hypothesis is pretty high. Therefore, the researcher doesn't conclude that students' attitudes are neutral about dorm living. Instead, the researcher concludes that there is not enough evidence to conclude that students are dissatisfied or satisfied with dorm living.
The hypothesis testing procedure just described is given called a
"t-test".
When using a t-test, the researcher computes a t-value.
One way to use the t-test for statistical decision
making is to compare this t-value to the appropriate critical value on
the t-distribution.
If the absolute value of the t-value is greater than the absolute
value of the critical t-value, then the null hypothesis is rejected.
The State University problem concerning dorm life is known as a "one
sample t-test" because the researcher is comparing the mean from one
sample to a given (often hypothetical) population mean.
The formula to compute the observed t-value when using the one sample
t-test is:
|
|
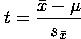 |
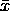 is the sample mean,
m is
the population mean, and s
is the sample mean,
m is
the population mean, and s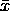 is the standard error.
is the standard error.
The t-value in a one sample t-test expresses the distance between the population mean and the sample mean in terms of the number of standard errors from the mean. You should recognize that the t-value is a standard score. If the observed sample mean equals the population mean, then the observed t-value is 0 bacause the sample mean is 0 standard error units away from the population mean. The further the sample mean is from the population mean, the greater the absolute value of the t-value. As the absolute value of the t-value increases, the more likely it is that the sample mean is truly different from the population mean, instead of being merely a result of sampling error.
Let's redo our example again, but instead of a sample size of
N = 15, lets assume that the researcher instead obtained
the same results using a sample size of
N = 20.
Again, we assume that the (theoretical) population mean is 4, the
sample mean is 5.0, and the sample standard deviation s
is 1.936.
Now, the standard error will be 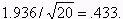 When N = 20, the critical value for a 5% significance
test will be 2.09 (because the t-distribution curve is closer to the
normal distribution).
The sample mean of 5.0 is now (5-4)/4.33 = 2.309 standard errors away
from the population mean of 4.
Thus, for a sample size of 20, the sample mean of 5.0 is significantly
different from the (hypothetical) population mean of 4.
Thus, the researcher can conclude, based on a sample size of 20, that
the dorm residents do in fact have non-neutral feelings about dorm life.
When N = 20, the critical value for a 5% significance
test will be 2.09 (because the t-distribution curve is closer to the
normal distribution).
The sample mean of 5.0 is now (5-4)/4.33 = 2.309 standard errors away
from the population mean of 4.
Thus, for a sample size of 20, the sample mean of 5.0 is significantly
different from the (hypothetical) population mean of 4.
Thus, the researcher can conclude, based on a sample size of 20, that
the dorm residents do in fact have non-neutral feelings about dorm life.
Finally, let's look at the State University problem more graphically. Again we assume that the population mean is 4 and the observed sample mean is 5.0. Examine the graphs and answer the questions in the right-hand box.
As explained above, the shape of the t-distribution is affected by sample size. As the sample size grows, the t-distribution gets closer and closer to a normal distribution. Theoretically, the t-distribution only becomes perfectly normal when the sample size reaches the population size. Nonetheless, for practical purposes, the t-distribution is treated as equal to the normal distribution when sample sizes are greater than 30. Thus, the t-distribution is actually a family of sampling distributions, because every sample size produces a slightly different t-distribution. It is technically more accurate, however, to state that t-distributions change as a function of degrees of freedom.
It is beyond the scope of this tutorial to explain the concept of degrees of freedom in detail. At this point, it is only necessary that you know degrees of freedom are directly related to sample size. As the sample size increases, so do degrees of freedom. When degrees of freedom are infinite, the t-distribution is identical to the normal distribution. As sample size increases, the sample more closely approximates the population. Therefore, we can be more confident in our estimate of the standard error because it more closely approximates the true population standard error. As we become more confident that our estimate of standard error approaches the true population value, the shape of the t-distribution approaches the shape of the normal distribution.
The applet below shows how the shape of the t-distribution comes to approximate the normal distribution as the degrees of freedom/sample size increases. Move the indicator on the slide bar to the left to decrease sample size and to the right to increase sample size. Notice that when the sample size is close to 30, it is difficult to differentiate the t-distribution from the normal distribution.
In the above exercise, you should realize that each time the sample
size changes, a different t-distribution appears.
This is illustrated by the fact that the red line has a different
shape for each value of N.
That's why the t-distribution is a family of sampling distributions.
The practical importance of this family of sampling distributions is
that the critical values for a given probability (e.g., .05) change
each time the sample size changes.
For example, when N = 11, the two-tailed, .05 critical
t-value is +2.228, but when N = 16, the
two-tailed, .05 critical t-value is +2.131.
The magnitude of the changes in critical t-values as a function of
sample size are greater when sample sizes are below 30.
Above 30, the changes in critical t-values as a function of sample
size are so small that they are not practically important.
Because the t-distribution is a family of sampling distributions, a
researcher must always report the sample size
used to test the hypothesis so that other researchers know
what critical t-values were used.
When testing hypotheses using a t-test, the critical t-value is determined by a researcher's willingness to make a Type I error and whether the hypothesis is two-tailed or one-tailed. Type I error is the probability of rejecting a true null hypothesis, that is, making the error of claiming that there is a significant difference between two populations when no such difference exists. Traditionally, researchers will only claim a result is significant if the risk of error is less than 5%. This means that when the observed t-value exceeds the critical t-value (i.e., the t-value marking that portion of the curve containing 5% of the area), the researcher will reject the null hypothesis, but in doing so, he/she is taking up to a 5% chance of claiming a significant difference when none exists. Of course, 5% is just an accepted rule of thumb. If a researcher wants to be highly cautious about making a Type I error, he or she can set a more conservative (i.e., smaller) Type I error rate such as 1%. If the researcher is less concerned about making a Type I error, he/she can set a more liberal (i.e., larger) Type I error rate such as 10%. As the Type I error rate changes so will the critical t-values. With a sample size of 20, the .05, two-tailed critical t-value is +2.093. However, at the more conservative 1% Type I error rate, the two-tailed critical t-value is +2.861 and at the more liberal 10% Type I error rate, the two-tailed critical t-value is +1.729. Notice how the critical t-value decreases as the researcher's willingness to erroneously reject a true null hypothesis increases.
The other factor affecting the critical t-value(s) is whether the alternative hypothesis is one- or two-tailed (see Hypothesis Testing tutorial for review of one-tailed and two-tailed hypotheses). To this point in the tutorial, all examples have used a two-tailed alternative. For example, in the State University example above the researcher was examining whether student satisfaction was either above or below neutral. This is a two-tailed test requiring both a negative and a positive critical value. Typically, the two-tailed test critical t-value is .05 (i.e., 5%). That results in an area of .025 (i.e., 2.5%) to the left of the negative critical value and .025 (i.e. 2.5%) to the the right of the positive critical value.
Often researchers have an idea of the direction of the difference from the null hypothesis and use a one-tailed significance test. For example, the researcher from State University may have knowledge that students weren't dissatisfied with dorm life. He or she could have stated the alternative hypothesis as the following directional hypothesis: Students at State University are satisfied with dormitory living. In this case, only observed sample means above the hypothetical neutral population mean supports the directional hypothesis. Therefore, the researcher puts all the Type I risk in the right tail of the t-distribution. That is, only one positive critical t-value is set and that critical t-value is set at the point where 5% of the area under the t-distribution falls to the right of the critical value. For example, when sample size is 20, the .05 critical t-value for a two tailed test is +2.093, but the critical t-value for a one tailed test is +1.792 (when the alternative hypothesis predicts the sample mean is greater than the population mean) or -1.792 (when the alternative hypothesis predicts that the sample mean is less than the population mean).
Below is an exercise that will graphically show how the area under the the t-distrubution that lies beyond the critical t-value changes as the hypotheses change from one-tailed to two tailed, and as changes are made to the risk of making a Type I error. The t-distribution below is for a sample size of 20. The box in the center of the t-distribution shows the total area of the t-distribution that lies beyond the upper and lower critical values (i.e., the total area of the shaded tails). You can change the critical t-values by simply dragging either the upper or lower critical t-value to the desired point. Work through the exercise by following the instructions and answering the questions that appear to the right of the figure.
The exercise above shows graphically what happens when researchers use a one sample t-test. In practice, researchers do not need to look at the graphics that underlie the use of the t-test. Instead, the researcher will usually enter the data into computer and use statistical software that computes the observed t-value and provides a probability of the observed t-value occurring assuming the null hypothesis is true. The researcher makes the statistical decision to reject or fail to reject by either comparing the observed t-value to the appropriate critical t-value, or equivalently by comparing the probability associated with the observed t-value against the researcher's risk level for making a Type I error.
While the single sample t-test is easiest to understand, it is rarely used in practice. That's because researchers don't often have a population mean to compare against an observed sample mean. A more common situation is to compare two different samples of subjects in order to decide if they come from the same population. Let's return to our State University example. Instead of deciding if student satisfaction with dormitory life is different from neutral, it is probably more useful for administrators to answer questions that make explicit comparisons. For example, are students living in co-ed dorms more or less satisfied than students living in single sex dorms? Are students at State University more or less satisfied with dorm living than students attending Small College?
For these comparisons, the null hypothesis is that the two samples can be treated as members of the same population for the variable of interest (e.g., satisfaction with dorm living). This hypothesis is often stated as m 1 - m 2 equals zero, where m1 refers to the mean of the first sample, and m 2 refers to the mean of the second sample. The alternative hypothesis states that the two samples come from different populations for the variable of interest and can be stated as m1 - m2 is not equal to zero (for the two-tailed test) or m1 - m2 is greater than zero (for the one-tailed test) or m1 - m2 is less than zero (for the one-tailed test in the other direction).
Note that the two samples must differ on some variable, such as "co-ed versus single sex dorms" or "attends State University versus Small College." The variables that distinguish the groups are often called independent variables. The null hypothesis predicts that two groups who differ on the independent variable can nonetheless be treated as the same population when it comes to the variable of interest (in our example, the variable of interest is satisfaction with dorm living). The alternative hypothesis predicts that not only do the two groups differ on the independent variable, they also should be treated as different populations with respect to the variable of interest. The variable of interest is often called the dependent variable.
As discussed in the example at the begining of this tutorial,
the researcher must rely on a sampling distribution to test the
hypotheses.
The graphic below shows the logic of creating the sampling
distribution for two independent samples.
The top of the graphic shows the population frequency distribution for
two populations that are differentiated by the independent variable.
For each of these two populations we select sample sizes,
referred to as n1 and n2.
Then a sampling distribution of the mean is generated for each
population.
To create a single sampling distribution, known as the sampling
distribution of the differences between the means, all possible
deviations between population 1 means and population 2 means are
computed.
These deviations are then plotted.
The bottom of the graphic shows the sampling distribution
of the differences between the means.
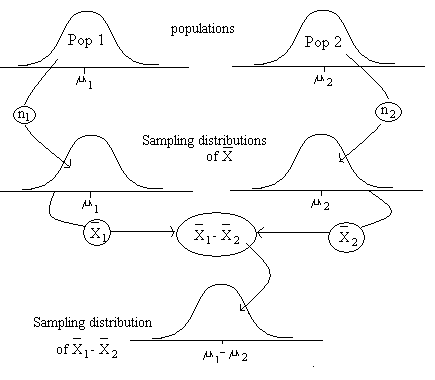
It is important to recognize the the mean for the sampling distribution of the mean is zero when the null hypothesis is true. That's because both populations have the same mean, which also means that both sampling distributions will have the same mean, therefore, the average deviation between the means will be zero. Remember that hypothesis testing always uses the sampling distribution associated with the assumption that the null hypothesis is true.
As the single sample t-test, the sampling distribution for
the difference between the means is also a t-distribution.
Further, the standard deviation (i.e., the standard error) of the
sampling distribution of the difference between the means must be
estimated because the decision to reject the null hypothesis is based
on how many standard error units the observed difference in the sample
means is from zero.
Fortunately, this standard error can be estimated.
Because we are now dealing with two samples this standard error is now
called the standard error of the difference instead of the standard
error of the mean.
The formula for the standard error of the difference is:
|
|
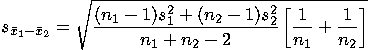 |
While this formula is complex, closer examination shows that the standard
error of the difference is simply a function of the sample size of the
two groups (i.e. n1 and n2) and the variance on the
dependent variable within the two groups (i.e., s12
and s22).
The computation of the observed independent samples t-value is also
more complicated because of using two samples.
The formula is:
|
|
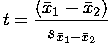 |
Independent sample t-tests are often performed when you want to know if members of certain subpopulations differ on a dependent variable. When we focus sampling efforts on specific parts of the population, this is called stratification. The following activity allows you to choose a variable and then divide a larger population into separate subpopulations that you believe would differ in terms of the variable you chose. Then you can collect a sample of size 50 from each population and compute sample statistics for each sample to determine if the difference between samples is significant. To start the activity, select a sub-population from the list and then click the "take a sample" button. Answer the questions that appear on the right side. This exercise doesn't use critical values to decide whether to reject the null hypothesis. Instead, answer the question of statistical significance by examining the probability that appears in the center of the figure. Treat each hypothesis as a two-tailed test with a .05 Type I error. (Hint: You should reject the null hypothesis when the percentage in the box in the center of the distribution is less than 2.5%.)
The above exercise is very similar to how a researcher uses an independent samples t-test. The only difference is that the researcher doesn't even look at the graphic picture. All the researcher needs to know is the percentage of scores in the sampling distribution fall beyond the observed t-value (i.e., the percent in the box in the center of the distribution). If that percentage is less than the researchers choice for Type I error, then the researcher will reject the null hypothesis.
For the independent samples t-test, the researcher is testing differences between the means of two different samples of subjects. Often, researchers are interested in how the same sample of subjects change over time or in response to some intervention. Returning to the State University example, lets say that administrators are planning to air condition the dormitories and they want to know what effect the air conditioning has on students satisfaction of dormitory life. In this case, the researcher could sample the same group of dormitory residents before and after the air conditioning is implemented.
A t-test is also used to determine if a true change in the mean response takes place. However, the sampling distribution is derived differently because the study uses the same group of subjects measured at two different points in time. In this case the t-test is known as the dependent sample t-test or what is often called the "paired sample t-test". We have already shown how the sampling distribution is derived for both the one sample and independent sample t-test. We will not repeat the derivation of the sampling distribution for the dependent sample t-test. Suffice it to say that it is similar to the way that the prior sampling distributions were derived and also results in a sampling distribution with a mean of zero (assuming the null hypothesis is true). Rejection of the null hypothesis is based on how many standard error units the observed differences between the means are from zero.
Using the State University example, let's walk through a paired t-test analysis. The null hypothesis is that the installation of air conditioning does not influence satisfaction with dormitory living. The alternative directional hypothesis is that the installation of air condition increased student satisfaction (i.e. a one-tailed test)
Suppose you have collected the following data.
|
|
Pre-installation satisfaction (A) | Post-installation satisfaction (B) | Difference (D) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
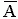 = 4.2 = 4.2 |
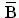 = 5.6 = 5.6 |
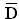 = 1.4 = 1.4 |
The question we need to answer is whether the mean difference of 1.4 is
sufficiently different from 0 to reject the null hypothesis.
Just like in other sampling distributions, the paired sample standard error
of the mean of difference (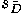 ) can be estimated using
a formula.
) can be estimated using
a formula.
|
|
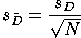 |
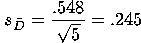
In the case of the paired t-test, the formula for calculating t is:
|
|
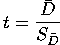 |
In our example, t = 1.4/.245 = .571.
The t-distribution is one of the most useful statistics available to a behavioral scientist. In this tutorial, you were shown how to conduct a one sample t-test, an independent sample t-test, and a paired sample t-test. The t-test can be adapted to many other statistical questions that have not been covered. For example, a t-test is also used to assess if correlation coefficients and regression coefficients are significantly different from zero. In short, a behavioral scientist must have good working knowledge of the various uses of the t-statistic because its use is so prevalent. Part of this good working knowledge is understanding the assumptions that one makes when using a particular t-test. For example, to use the independent samples t-test presented above, it must be assumed that the variance in Population 1 is equal to the variance in Population 2. A good researcher will check the validity of important assumptions associated with the statistical test before testing the hypothesis.
Having completed this tutorial, you should have a general understanding of:
Return to Table of Contents