Hypothesis Testing
All files, sofware, and tutorials that make up SABLE are
Copyright (c) 1997, 1998, 1999 Virginia Tech.
You may freely use these programs under the conditions of the
SABLE General License.
Hypotheses About Populations
Scientists often try to answer questions about populations.
Let's assume that for some reason a researcher believes 6th graders in
Virginia possess, on average, a different level of intelligence from other
6th graders in the United States. In essence, this researcher is attempting
to determine if Virginia 6th graders should be considered a different population
than the U.S. population of 6th graders (outside of Virginia) on the dimension
of intelligence.
Below are three graphic representations of what the true situation might
be when comparing Virginia 6th graders to the U.S. population of 6th graders.
The larger, red curve represents the population distribution of intelligence
scores for 6th graders in all states other than Virginia. The smaller,
blue curve represents the population of intelligence scores for Virginia
6th graders. The greek letter m represents the
mean of a population.
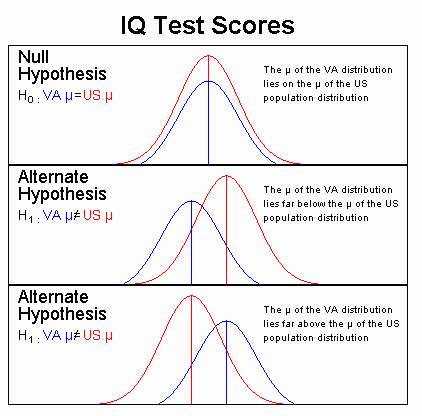
If the top picture is true, then there is no difference between the
population means, and Virginia 6th graders are not a different population
from 6th graders from outside Virginia. If either the middle or bottom
pictures are true, however, then for intelligence Virginia 6th graders
are a different population from U.S. 6th graders outside of Virginia. In
these cases, Virginia 6th graders would be a different population because
their average intelligence is either less than (the middle picture) or
greater than (top picture) the U.S. population of 6th graders. These three
pictures exhaust the possibility of answers to the question in that the
Virginia population's intelligence is either equal to, less than, or greater
than the U.S. population.
Sampling and Testing Hypotheses about Populations
Researchers typically do not have the luxury of collecting data on every
member of a population. Instead, they collect samples
from populations
and use the sample information to test hypotheses concerning the population
as a whole. In the present case, the researcher in this example will not
measure intelligence scores for every sixth grader in Virginia. It's more
likely that the researcher will only administer an intelligence test to
a sample of Virginia 6th graders. Furthermore, this researcher is unlikely
to measure the intelligence of any sixth grader outside the state of Virginia.
Instead, he/she probably will use an estimate for the average intelligence
of U.S. 6th graders. Let's assume that our hypothetical researcher has
collected intelligence scores on a sample of 50 Virginia students and that
the mean intelligence score for the U.S. sixth grade population is 100
points.
Given this information, one way to answer the question is to examine
the distribution of scores for the sample of Virginia students in relation
to the 100 point population mean intelligence score of U.S. 6th graders.
In making this comparison, the researcher examines how the population mean
is different from the sample mean of Virginia 6th graders. However, because
the intelligence of Virginia 6th graders is represented by a sample, the
researcher can never be 100% certain that he/she can make the correct decisions
about the hypotheses. That is, it is possible that the sample of scores
for Virginia 6th graders does not accurately reflect the distribution of
intelligence scores for the population of Virginia 6th graders. Therefore,
decisions based on the sample may lead to an erroneous conclusion about
the population. The extent to which a sample distribution is different
than the population distribution from which the sample is drawn is known
as sampling
error.
The dilemma faced by the researcher is to try and answer a question
when using sample data that contains some unknown amount of sampling error.
Fortunately, our researcher knows that the further the Virginia sample
mean score is from the U.S. population mean score, then the more likely
that the intelligence of the Virginia population of 6th graders is different
from the intelligence of the U.S. population of 6th graders. That is, small
differences between the Virginia sample mean and a U.S. population mean
are likely due to sampling error. When faced with small differences, the
researcher should conclude that there is not enough evidence to say that
the two populations are different. If the Virginia sample mean is far away
from the U.S. population mean, then it is unlikely that the difference
is due to sampling error. In this case, the researcher should conclude
that the Virginia population of 6th graders is different than the U.S.
population of 6th graders on the dimension of intelligence. In doing so,
the researcher is saying that he/she is confident that his/her findings
were not due to sampling error.
Let's see if you can think like a researcher!
Making Decisions about
Samples and Populations
Below are two possible distributions of intelligence scores for samples
of 50 Virginia 6th graders. The U.S. population mean of 100 is also marked
on each of the Virginia sample distributions. For each distribution, compare
the Virginia sample mean to the U.S. population mean and conclude whether
the Virginia population is the same as or different from the U.S. population.
Then, click on the appropriate button and see if you are correct.
Now that you have the idea, let's look at some real data sets. We will
assume that each distribution shown truly is the population distribution.
You can compare the population mean to the mean of a random sample. As
a scientist, you must determine whether or not the sample was drawn from
that population or some other population.
Making Decisions
The histogram (graph) below shows a distribution of ages for a group
of urban males. The black arrow points to the mean of this distribution,
The red arrow indicates the mean age of a sample, and you must decide whether
that sample comes from the same population whose distribution is shown,
or from some other population. Click the button to see if your decision
is correct. Choose different variables from the list and see how good you
are at making correct decisions.
If you selected a few variables in the above exercise, chances are you
made some erroneous decisions. One mistake that you likely made was to
conclude that the sample came from a different population when in fact
the sample came from the shown population. This mistake is called a
Type
I error. A second possible mistake is that you concluded that the sample
came from the shown population when in fact the sample came from a different
population. This mistake is called a
Type
II error. In research, the goal is to avoid making a Type I or Type
II error.
To this point we have used only our "eyeball" judgments of distributions
to guide decisions about whether the populations are different. In practice,
researchers rarely rely on such eyeball judgments because they are too
imprecise, leading to the Type I and Type II errors that researchers want
to avoid. Researchers are more likely to use quantitative indicators to
guide decisions about hypotheses because they are more precise, and thereby
reduce the the number of Type I and Type II errors. These quantitative
indicators are collectively referred to as "statistical significance tests".
All statistical significance tests are based on probability statements
about the likelihood of the observed findings. But before you can determine
the significance, you must first understand the concept of a sampling
distribution.
Introduction to Sampling Distributions
For any given population, a
sampling
distribution consists of all possible distinct samples that can be
drawn, given a constant sample size. The term distinct samples means that
a given sample from the population cannot be represented in the sampling
distribution more than once. If the population consists of A, B, and C,
and the sample size is two, then there are three distinct samples that
can be drawn: (A, B), (A, C) and (B, C). There is a finite number of distinct
samples that make up a sampling distribution. Let's return to our Virginia
sixth grader example. Assume for the sake of argument that the population
of Virginia sixth graders consists of only six students. Assume further
that their intelligence scores are:
|
Name:
|
Intelligence Score:
|
|
Bob
|
70
|
|
Amy
|
85
|
|
Lee
|
100
|
|
Robin
|
100
|
|
Kathy
|
115
|
|
Jack
|
130
|
With such a small population, it is easy to create a sampling distribution.
Now, let's create a sampling distribution of mean intelligence. The distribution
will contain sample means for all possible distinct samples.
Creating a Sampling Distribution
Create a sampling distribution for our hypothetical population of six
Virginia students. Click on any pair of names in the list on the left-hand
side. The mean intelligence score of this pair of students will appear
in a figure on the right-hand side. Continue to click on pairs of names
(in any order) until all fifteen pairs are plotted on the figure. Watch
how the mean and standard deviation change as you add pairs of names. Repeat
the exercise a couple of times, entering the pairs of names in different
orders.
When you have all fifteen pairs of names plotted, you will have the
sampling distribution of the mean for samples of size 2. All possible mean
scores for distinct samples of 2 in the population will have been plotted.
The overall mean of a sampling distribution of the mean is equal
to the mean of the population.
The standard
deviation of a sampling distribution is important because it indicates
how well the mean represents the population. The larger the standard deviation,
the less representative the mean will be. We can also describe this property
in terms of sampling error. The larger the standard deviation of the sampling
distribution, the greater the effects of sampling error. Sampling error
is critical when making conclusions based on a single sample of subjects.
Standard deviations of sampling distributions are so important that they
have the special label of standard
errors. Because the above sampling distribution is based on sample
means, the standard deviation of this distribution is known as the
standard
error of the mean.
The Effect of Changing
Standard Error
This exercise demonstrates the relationships between the range and
shape of the sampling distribution; the standard error of the mean (symbolized
as sm); and sampling error. Follow
the instructions appearing in the box on the right side.
A sample in a sampling distribution with a smaller standard error likely
will have less sampling error than a sample in a sampling distribution
with a large standard error. Smaller sampling error is important for two
reasons. First, the smaller the sampling error the more likely that a sample
statistic is a good estimate of the corresponding population statistic.
This quality is seen in the above exercise when the sample means clustered
closer to the population mean as the standard error decreased. Second,
and more importantly for hypothesis testing, the smaller the sampling error,
the easier it is to conclude that the sample statistic represents a different
population. This is because when sampling error is small, a sample mean
that is far away from the population mean almost certainly comes from a
different population.
Sample size is a primary determinant of sampling error, and hence the
magnitude of the standard error. The exercise below shows the effect that
increasing sample size has on the sampling distribution.
The Effect of Changing
the Sample Size
Here is the frequency distribution of sample means of the six students
(i.e., Bob, Amy, etc.) whom we treated as a population of Virginia sixth
graders. Remember, this is the sampling distribution when the sample size
is two. Change the sample size by clicking on the circles beside the numbers
on the right-hand side. Notice how the range of the distribution changes
as the sample size increases or decreases. This change in range is also
reflected in changes in the standard error of the mean shown on the lower
right.
In the above exercise, you should have noticed that the standard error
of the mean was zero when the sample size was six. That's because the entire
population of six students is used to compute the mean, therefore, there
is no sampling error! Recalling that small sampling error is desirable,
this shows why researchers usually strive to collect as large a sample
as is economically feasible. Again, one reason that small standard errors
are desirable is that sample statistics more accurately represent population
statistics when the standard error is small. As seen in the above exercise,
the distributions of mean scores clustered closer to the population mean
of 100 as sample sized increased, which shows that the sample means more
accurately estimated the population mean. Also, it is easier to detect
when samples do not come from the population at hand when sampling error
is small. For example, the score of 115 is contained in the sampling distribution
when the sample size is two, but is well outside the sampling distribution
when the sample size is four. Therefore, a mean score of 115 for two new
students could not be readily detected as representing a different population
than our original population of 6th graders. However, a mean score of 115
for four new students would indeed indicate that a different population
of 6th graders was sampled.
To summarize this section, you should now understand that the amount
of sampling error is indicated by the standard error and that small standard
errors are more desirable than large standard errors. Finally, the simplest
way to ensure a small amount of sampling error is to take as large a sample
as is economically feasible.
Using Sampling Distributions to Test Hypotheses
Let's examine the use of a sampling distribution for testing a hypothesis.
Assume enough research has been conducted in other states to estimate that
the population of intelligence scores for U.S. 6th graders is
normally
distributed, with a mean of 100 points and a standard error of the
mean (i.e., sM) of 5 points when
the sample size is 50. This sampling distribution is shown below. Assume
a sample of 50 Virginia 6th graders is tested for intelligence. The Virginia
sample mean then can be plotted on the population sampling distribution.
Sample Means and Sampling
Distributions
In the exercise below, we have set the mean to 100 points for this
hypothetical sample of Virginia 6th graders. Follow the instructions in
the panel on the right.
The term
confidence
interval is the generic label used to describe the decision points
where the researcher favors one conclusion over another. Traditionally,
researchers are very cautious about concluding that a sample is different
from the comparison population. In our example, our researcher would be
very cautious about concluding that Virginia 6th graders are different
from the U.S. population of 6th graders. Another way to describe this cautiousness
is to state that researchers are reluctant to make a Type I error. Typically,
a 95% confidence interval is set. A 95% confidence interval means that
if Virginia 6th graders are the same as U.S. 6th graders, then there
is only a five percent chance that the Virginia sample mean would fall
above or below the boundaries of the confidence interval. If the Virginia
sample mean is above or below the 95% confidence interval boundaries, the
researcher will conclude that Virginia 6th graders represent a different
population in terms of intelligence. If the Virginia sample mean falls
within the 95% confidence interval boundaries, the researcher will conclude
that there is not enough evidence that Virginia 6th graders are a different
population than U.S. 6th graders in terms of intelligence.
Sampling Distribution, Probabilities, and Critical Values
When discussing the percentage of scores above or below the critical scores
of a confidence interval, we are also making a probability statement. In
the case of the traditional 95% confidence interval, there is a .05 or
5% probability that the Virginia sample mean will fall above or below the
boundaries of the confidence interval, if Virginia 6th graders are the
same as U.S. 6th graders in terms of aptitude. This is the crux of
statistical significance -- if we obtain an estimate that occurs outside
the 95% confidence interval, then we conclude that our sample estimate
is significantly different from the population. We may be wrong to conclude
that the sample comes from a different population, but there is only a
.05 probability that we will make this Type I error.
Statistical Significance
The following distribution illustrates the relationship between the
boundaries of a confidence interval and statistical significance. The shaded
area designates the 95% confidence interval on a hypothetical sampling
distribution. Sample means that occur within the shaded region would lead
to the conclusion that the sample cannot be treated as coming from a different
population while values that occur outside of the shaded region would lead
to the conclusion that the sample comes from a different population.
The values that establish the boundaries of the confidence interval
are given the special name of critical
values. For our Virginia sixth grader example, 109.8 was the upper
boundary critical value and 90.2 was the lower boundary critical value.
However, it is not efficient to express critical values in terms of the
measuring scale used for the variable of interest because the critical
value would change every time a variable with a different measuring scale
is studied. To avoid having to list a different critical value every time
a different variable of interest is used, researchers express critical
values as z-scores
or standard scores. In that way, the same critical values are used for
the 95% confidence interval regardless of the measuring scale for the variable
of interest. In our example, the sampling distribution of the mean is normally
distributed and z = +1.96 is the upper boundary critical value and z =
-1.96 is the lower boundary. The +1.96 is the critical value because
2.5% of the means in the sampling distribution will be higher than +1.96
standard deviations above the mean and 2.5% of the means will be lower
than -1.96 standard deviations below the mean.
Critical values are not etched in stone; they will change as a function
of both the risk a researcher is willing to take on making a Type I error
and the shape of sampling distribution. As to the risk issue, the more
risk a researcher is willing to take on making a Type I error the smaller
the critical values. For a 90% confidence interval (a 10% chance of making
a Type I error) the critical values are +1.64. The less risk the
higher the critical values. For a 99% confidence interval (a 1% chance
of making a Type I error) the critical values are z = + 2.57. While
the sampling distribution used as an example earlier in this tutorial is
normally distributed, most sampling distributions are not normally
distributed. The critical values for the 95% confidence interval are different
for these non-normal sampling distributions than the +1.96 seen
for normally distributed sampling distributions. See the t-distribution
tutorial for an explanation of why the shape of a sampling distribution
is not always normal.
Two-Tailed Tests Versus One-Tailed Tests
The example we have been working with is known as a two-tailed hypothesis
test. It is a two-tailed test because we are looking to see if Virginia
6th graders are more or less intelligent than U.S. 6th graders.
Therefore, we set a critical value in both tails (i.e., a two-tailed test)
of the sampling distribution. In a one-tailed test, the researcher has
an expectation as to the direction of the difference. Perhaps the researcher
in our example has some evidence to suggest that Virginia 6th graders are
smarter than the U.S. population of 6th graders. In this situation, the
researcher will not only predict that Virginia sixth graders are different,
he/she will also predict the direction (often called a directional prediction)
of the difference (e.g., Virginia 6th graders are smarter than U.S. 6th
graders). This is known as a one-tailed hypothesis test because only scores
in one tail of the sampling distribution will lead the researcher to conclude
support for his/her directional prediction. Assuming our researcher is
only willing to risk a .05 or 5% chance of a type I error, he/she will
set the critical value where only 5% of the scores in the sampling distribution
fall above the critical value. In our example, the critical value for this
one-tailed test is +1.64.
Directional/Nondirectional
Hypotheses and Risk
This distribution of sample means has "tails" marked in black. The
numbers tell the percentage of the area under the curve that lies outside
the shaded region. Use the information shown to answer the multiple choice
questions.
Review Definitions:
Type I Error,
Type II Error.
Formal Hypotheses
In science, research questions are formally stated, before a study is
done, as a prediction that contains two parts. The first part of the
prediction is known as the null
hypothesis. It is called the null hypothesis because this is the prediction
that the researcher wishes to 'nullify'. Often in the behavioral sciences,
the null hypothesis is a prediction that there is no difference between
groups. The null hypothesis is symbolized as H0. For example,
the null hypothesis for the research issue regarding Virginia 6th graders
is
H0: Intelligence of Virginia 6th graders
equals the Intelligence of U.S. 6th graders
The second part of the formal prediction is known as the
alternative
hypothesis (often symbolized as H1). In the behavioral sciences,
the alternative hypothesis is usually the hypothesis the researcher expects
the data to support. The alternative hypothesis in the behavioral sciences
usually predicts a difference between groups. In the above example, the
researcher believes that Virginia intelligence scores are different than
U.S. intelligence scores; therefore, the alternative hypothesis is
H1: Intelligence of Virginia 6th graders
does not equal the Intelligence of U.S. 6th graders
When the alternative hypothesis simply states that there is a difference
between groups, like the alternative hypothesis in this example, it is
called a nondirectional alternative hypothesis, and a two-tailed significance
test (with critical values in both tails of the sampling distribution)
is used. The hypothesis is nondirectional because the alternative hypothesis
is supported whether the Virginia mean is above or below the U.S. mean.
If for some reason, the researcher in this example believes that the intelligence
of Virginia 6th graders is higher than the intelligence of other U.S. 6th
graders, then the alternative hypothesis is written as:
H1: Intelligence of Virginia 6th graders
is greater than the Intelligence of U.S. 6th graders
This is a directional alternative hypothesis because it predicts the direction
in which the difference will occur and a one-tailed significance test,
with only one critical value, is used. Similarly, if the researcher believes
that the intelligence of Virginia 6th graders is lower than the intelligence
of other U.S. 6th graders, then the directional alternative hypothesis
is written as:
H1: Intelligence of Virginia 6th graders
is less than Intelligence of U.S. 6th graders
When using statistical significance testing, if the sample statistic lies
outside the confidence interval then the researcher "rejects the null hypothesis"
in favor of the alternative hypothesis. If the sample statistic lies within
the boundaries of the confidence interval, then the researcher "fails to
reject the null hypothesis". The rather strange wording of "fail to reject"
is used because researchers don't conclude the null hypothesis is true.
Rather, they consider that not enough evidence exists at this time to reject
the null hypothesis.
Making Decisions about
Statistical Significance
The following exercise integrates statistical significance testing
with decisions about formal hypotheses. The red line on the distribution
corresponds to the sample mean.
More on Making Decisions
About Statistical Significance
Let's repeat a prior activity where you used "eyeball" judgments to
determine if the sample mean was drawn from the same or different population
for many different variables. This time, however, you will treat the problem
as a statistician would. The question will be stated in terms of the formal
null hypothesis, which you will be asked to "reject" or "fail to reject".
Also, to aide your decision, the sampling distribution of the mean is overlayed
in blue on the frequency distribution. Examine the sample mean in
relation to the sampling distribution of the mean. This relationship
is quantified by the probability value appearing below the sample mean.
When the sample mean is above the population mean, this probability tells
you what percent of the sample means in the sampling distribution are equal
to or greater than the observed sample mean. When the sample mean
is less than the population mean, this probability tells you what percent
of the sample means in the sampling distribution are equal to or less than
the observed sample mean. Use a two-tailed 95% confidence interval
whereby you only reject the null hypothesis if the probability value is
less than .025. When you use the probability in this manner you are performing
a statistical significance test!
There are many issues surrounding how sampling distributions are used
in hypothesis testing that are not covered here. First, although the above
examples were based on a sampling distribution of the mean, it is important
that you realize that a sampling distribution can be created for any statistic.
For example, a sampling distribution can be created for standard deviations
or for correlation coefficients. Although sampling distributions can be
created for a multitude of statistics, the logic of sampling distributions
as applied to research is the same. Second, the above example was predicated
on the assumption that the population parameters for the U.S. 6th graders
(i.e., mean and standard deviation) were known to the researcher. The fact
is that a researcher rarely knows the population parameters. Other tutorials
will deal with how researchers get around this problem of unknown parameters.
In summary, this tutorial has introduced the role of sampling distributions
in hypothesis testing. Upon completion of this tutorial, you should have
a general understanding of:
-
Sampling Distributions
-
The importance of the mean of the sampling distribution
-
The importance of the standard deviation of the sampling distribution
-
Type I error
-
Type II error
-
Why smaller standard errors are better than larger standard errors
-
Why larger sample sizes produce smaller standard errors
-
The importance of standard errors in hypothesis testing
-
Confidence Intervals
-
Critical Values
-
Two-Tailed Hypothesis Tests
-
One-Tailed Hypothesis Tests
-
Null Hypothesis
-
Alternative Hypothesis
-
Directional Hypothesis
-
Rejecting the Null Hypothesis
-
Failing to Reject the Null Hypothesis
Go to Top of Page
Return to Table
of Contents
Report Problems to SoSci
Updated December 2, 1998

