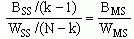
This tutorial presents a way to test for significant differences among sample means when the independent (predictor) variable is a set of discrete categories, and the dependent variable is continuous, ordinal, or dichotomous. Called ANalysis Of VAriance, or ANOVA, it can be used, for example, to test the null hypothesis that plumbers, electricians, and carpenters all have roughly the same average income. The null hypothesis is that the sample means are so similar that they have been obtained by drawing samples from the same population. That is,
H0: m1 = m2 = m3 = ... = mk.
Note that the t-test would have been used if the null hypothesis had concerned only two groups. In the t-test tutorial we examined comparisons of a single sample mean with the population mean and of two sample means with each other. In this tutorial we will be concerned with situations in which three or more sample means are compared with each other to test for statistically significant differences among those means and, in turn, among the means for their populations. ANOVA should be viewed as an extension of the t-test, to be used when there are more than two comparison groups.
This tutorial examines one-way ANOVA, in which there are three or more comparison groups each representing a category of a single predictor variable. It is possible to extend the logic of ANOVA to investigate the impact of two or more predictor variables considered simultaneously. An example would be the impact of occupation and region of the country on income. Such analysis is referred to as "two-way ANOVA" or "three-way ANOVA" or, more generally, "multiple analysis of variance."
The present tutorial is restricted to one-way ANOVA and will focus on the following concepts:
ANOVA is a technique for testing the hypothesis that sample means of several groups are derived from the same population. Let us consider an example. Suppose that you are a Quality Assurance Supervisor at Boxes, Inc., in Utica, New York. You have been instructed to have four of your factories, located in Alaska, Deleware, Georgia, and Maine, make boxes for your company. However, Boxes, Inc. does not have a quality control department at any of the factories. Consequently, box samples must be shipped to the head office in New York so that they can be inspected before being shipped to customers. As part of the inspection, you must ensure that the four factories produce roughly the same output. If the processes for making the boxes are the same in each factory, then there should not be much variation in the size or other characteristics of the boxes. However, if the processes do differ appreciably, then there may be statistically significant differences in the average size of boxes made in those four factories. Data on the volume of the boxes can be used to test the null hypothesis that the average volume of the boxes does not vary significantly from factory to factory.
To decide whether or not the factories produce similar output, we are fundamentally concerned with the question of whether the differences (variance) in the boxes made within each factory are "large" compared to the differences (variance) in the means for the boxes made at the different factories. In essence, an ANOVA computation boils down to comparing the variances among the means to the variances within the samples. What it takes to be "large enough" for the difference to be statistically signficant depends on the sample sizes and the amount of certainty that we desire in our testing (that is, p values or levels of statistical significance that we typically use with all of our significance tests).
We now examine the process by which an ANOVA calculation is done. We will begin by filling in an ANOVA table. Among other things, an ANOVA table stores the arithmetic mean for each sample, along with the between-groups sum of squares and the within-group sum of squares. In the table below, "Mean" refers to the arithmetic mean of all the box samples from some factory. "Within-group Sum of Squares" (WSS) is the sum of squared deviations of each box size from its sample mean. The "Between-groups Sum of Squares" (BSS) is the sum of squared differences of each of the sample means from the mean for all of the boxes in all of the samples under consideration. Taken together, BSS and WSS equal the "Total Sum of Squares" (TSS) which is the sum of squared deviations of all of the individual cases in all of the samples from the arithmetic mean for all of those individual cases. As will be explained in greater detail, the likelihood of the sample means being found to differ significantly from each other increases as the average BSS grows large relative to the average WSS and as the sample sizes increase. These two conditions mirror those that result in statistical significance in the t-test.
Begin the following activity by clicking on the button labled "start" that is at the bottom of the activity. The computer will then sum down all boxes produced in Alaska to compute the mean volume of the boxes produced in Alaska, and the WSS, or the sum of squared deviations of each individual box size from the state mean box size. Click the button (now labeled "next") to repeat these computations for each of the other states. After computing the mean and the WSS for each state, click the button again to add the WSS across all states. Click the button a final time to compute the BSS, or the sum of squared differences of each of the state means from the mean for all of the cases in all of the samples under consideration, and the TSS.
Activity 1A
Recall that our chief concern in determining whether the samples are likely to have been drawn from different populations or not is deciding whether the differences between the samples is greater than the differences within the samples. Now that we have the WSS and BSS values, we can proceed to the step of comparing them.
To evaluate whether the BSS is large relative to the WSS, it is necessary to take into account the number of independent scores, or degrees of freedom (d.f.) that contribute to each of those sums. For the BSS, d.f. = k-1 where k is the number of comparison groups. In estimating the overall population mean from the set of sample means, one degree of freedom is lost because, once all but one of the sample means is known, assuming the size of each sample is also known, then the mean for the kth sample is fixed. For the WSS, d.f. = N - k. One degree of freedom is lost in calculating the sample mean for each of the k samples, for a total of N - k degrees of freedom lost in calculations of the WSS. The degrees of freedom for TSS is (k - 1) + (N - k) = N - 1.
We now define the F-ratio as
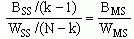
Here, BMS and WMS refer to the "Between-Groups Mean Squares" and "Within-Groups Mean Squares," respectively. Each of these MS values is an estimate of the variances in what is conceived of as a total population from which the various samples were drawn. BMS is an estimate of the variance for the several sample means, and WMS is an estimate of the variance of the scores from their respective sample means. If differences across sample means are "large" relative to differences within samples, then we should reject the null hypothesis that the samples are all drawn from the same population.
Activity 1B
To begin Activity 1-B, click on the "Get Data" button. This will retrieve the BSS, WSS, and TSS that were computed in Activity 1-A. Then, click the "Step 1" button to calculate the degrees of freedom for the BSS, WSS, and TSS. Next, click the "Step 2" button to compute the MS values. Finally, click the "Step 3" button to compute the F Ratio of these MS values. The last step is to transfer this information to the ANOVA Table at the bottom of the activity. Click on the "Compute" button to complete the transfer.
As noted above, F is the ratio of two estimates of variance calculated from the individual scores under consideration. F is the ratio of the BSS divided by its degrees of freedom to the WSS divided by its degrees of freedom. This ratio can be thought of as addressing the questions, "Are the differences among sample means large? Are they large relative to a meaningful baseline? What is that baseline?" This last question carries us to the essence of what ANOVA is all about: "Do the sample means show differences from each other that are large relative to the differences among individual cases within each sample?" This will become more apparent in Activity 4.
Before proceeding, we must note that strictly speaking, the F-test for differences among three or more means is truely valid only when (i) the samples are independently drawn from a normal population, and (ii) the variances within all of the samples are roughly comparable. In actual practice, the F-test has been found to work well even when these assumptions are not met, unless the departures from those assumptions are very large.
The decision of whether or not to reject the null hypothesis that the sample means are similar to each other requires that the value for F be compared with a critical value. And, in turn, just as for the t-test, the critical value differs with the number of degrees of freedom. Unlike the t-test, the critical value of F needed to reject the null hypothesis at any given level of significance (e.g. .05, .01, or .001) varies with two rather than only one indicator of degrees of freedom. The alpha level of F for rejecting the null hypothesis depends on both the Between and the Within gropus degrees of freedom.
An additional difference between the t and F tests is
that t-tests are commonly used in one-tailed tests that are
directional
(e.g. electricians' average income is higher
than plumbers' average income) as well as in two-tailed tests that
are non-directional tests
(electricians' average income differs from plumbers'
average income).
By contrast, in general, the F test
is used in non-directional tests.
That is, the
alternative hypothesis
is that
m1  m2
m2  m3
m3  mk.
The question we will address is strictly whether the means differ from each
other.
Nonetheless, it is possible to test more specific alternative
hypotheses.
For example, the null hypothesis could be that electricians, plumbers,
and carpenters all have comparable mean income; and the
alternative hypothesis could be that electricians have higher
income than either carpenters or plumbers.
Such directional tests lie beyond the scope of this tutorial.
mk.
The question we will address is strictly whether the means differ from each
other.
Nonetheless, it is possible to test more specific alternative
hypotheses.
For example, the null hypothesis could be that electricians, plumbers,
and carpenters all have comparable mean income; and the
alternative hypothesis could be that electricians have higher
income than either carpenters or plumbers.
Such directional tests lie beyond the scope of this tutorial.
Each of the next three activities will demonstrate one of three different influences on the F Ratio: the variance of values within each group, the variance of values between groups, and the sample size of each group.
The activities which follow display the distribution of observed values on an imaginary dependent variable for each of three independent variable categories, the "green group", the "turquoise group", and the "blue group".
Activity 2
This activity displays how the differences in the observed group means
is related to the Between Groups Sum of Squares and Mean Square, and how
the Between Group Sum of Squares and Mean Square are related to F.
Start by clicking on the button for the green group.
Then use the scroll bar below the distribution to move the
distribution of scores for the green group.
Move the distribution so that the mean for the green group is equal to
50.
Then, repeat this process for the blue group and the turquoise group,
so that all group means are equal to 50.
Next, try separating the groups as much as possible: shift the groups so
that the mean for the green group is equal to zero, the mean for the
blue group is equal to 50, and the mean for the turquoise is equal to
99.
Observe how the Between Groups Sum of Squares and Mean Square changes,
as well as how the F ratio changes.
As you can see, the greater the difference among the means, the higher the F and the greater the likelihood of rejecting the null hypothesis. It is important to note that a large F does not by itself convey why or how the means differ from each other. A high F value can be found when the means for all of the groups differ at least moderately from each other. Alternatively, a high F can be obtained when most of the means are fairly similar but one of the means happen to be far removed from the other means. You can see this in the example above if you position the green group and the turquoise group so as to have nearly identical means, but you position the blue group to have a mean which is far removed from both the green and the turquoise groups.
In the next example, it will be shown how the variability of observed scores within each group also influences the F ratio.
Activity 3
This activity displays how the variability of scores within each group is related to the Within Groups Sum of Squares and Mean Square, and how the Within Group Sum of Squares and Mean Square are related to F. It allows you to control the variability of scores within each group by using the vertical scroll bar on the right side of the display. Start by clicking on the round button which corresponds to the blue group. Then use the scroll bar to minimize the within group variances. Adjust the distribution of scores for the blue group so that the standard deviation of the score distribution is equal to 1. Then, repeat this process for the green group and the turquoise group, so that all group standard deviations are equal to 1. Next, maximize the within group variance. Adjust the distribution of scores so that the standard deviations of the score distributions for each group is equal to 10. Observe how the Within Groups Sum of Squares and Mean Square changes, as well as how the F ratio changes.
Hopefully, the previous example made clear that not only is the F ratio influenced by group means, but it is also influenced by the distribution of scores within each group. Using our hypothetical example based on group colors, if you are saying that group color influences scores on the dependent variable, then not only do the means of the groups differ from each other, the observations of the blue group members should be reasonably close to each other - that is, there should not be a great deal of Within Group variability. We will revisit this idea in Activity 5 below. But first, we need to consider a final influence on the F ratio - the sample size of each group.
This activity displays how the sample size of each group is related to the Within Group Mean Square, and how the Within Group Mean Square is related to F. It allows you to control the sample size of each group by using the up and down arrows of the sample size control marked "n". Start by clicking on the round button which corresponds to the green group. Then use the sample size control to increase the size of the green sample to 25. Repeat this process for the blue group and the turquoise group, so that all group sample sizes are equal to 25. Next, decrease the size of each sample so that there are 10 observations in each group. Note what happens to the Between Groups Sum of Squares, the Within Group Sum of Squares, the Between Groups Mean Square, the Within Groups Mean Square, and the F ratio as you change the sample size.
Now that you have seen the three influences on the F ratio, let's put all this information together. The example below allows you to control the group mean differences, the variability within each group, and the sample size. Adjust the magnitude of the group mean differences, the within group variability, and the sample sizes, and observe how each change influences the Between Groups Sum of Squares and Mean Square, the Within Groups Sum of Squares and Mean Square, and the F ratio.
Now that we have examined the various influences on the F Ratio, it is time to examine how we know when an observed F ratio is large enough to lead us to reject the null hypothesis. As was mentioned above, evaluation of the F ratio is a function of two indicators of degrees of freedom, the degrees of freedom used to compute Between Groups Sum of Squares, and the degrees of freedom used to compute Within Groups Sum of Squares. The observed F ratio is compared to the critical F values for a given alpha level and degrees of freedom combination. The activity below allows you to adjust the Between Groups degrees of freedom and the Within Groups degrees of freedom, and observe the resulting effect on the distribution of F. In addition, the table below the F distribution displays the critical values of F for each degrees of freedom combination which you select.
Activity 5
Activity 6
Return to Table of Contents